You are currently viewing Convex Recoloring of Trees and Networks

Convex Recoloring of Trees and Networks

Convex Recoloring of Trees and Networks

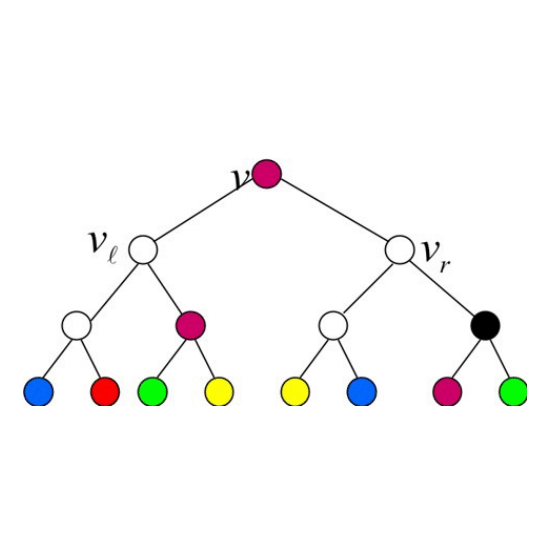
Definition: Given a necklace of colored beads, we say that the string is convex if all beads of the same color are in one chunk. In graph theory terms, we can view the necklace as a path and the coloring C as function from V to the set of colors C . Then C is convex if every subset of vertices belonging to the same color class is connected . 
However, when the coloring is not convex, we would like to find the closest coloring C’ that is convex. This distance between the two colorings C’ and C depends on the model assumed. Under the simplest model this is just the number of vertices whose color is changed between C’ and C . It can be shown that under this model, it is enough to uncolor this set of vertices and obtain a partial convex coloring. 
For further details see publications.

History: The motivation to the problem came from phylogenetics (The description of the evolution of a group of species by a tree , see e.g.Charles Darwin’s Origin of Species (publ. 1859)). At this first stage, we considered only total C(i.e. all vertices are colored). However, very shortly we noticed that the problem very elegantly and naturally generalized to partial coloring, or specialized to a simple path or leaf colored trees. 
The proof of hardness of the simplest case, led to the developments of approximation and fixed parameter algorithms (FPT) for various types of the problem. 
CR has been the subject of M.Sc. and Ph.D. students around the world.

Contest: The developments of FPT algorithms for the problem drew Mike Fellows’es interest. CR is now featuring in the FPT community (along with VC, FVS, etc.) as a target to a race for the fastest FPT algorithm.

CR fig2.jpg
CR fig1.png.jpg
 

  1. S. Moran and S. Snir, Convex Recolorings of Phylogenetic Trees: Definitions, Hardness Results and Algorithms. Journal of Computer and System Sciences (JCSS). 74(5): 850-869 (2008). 

  2. S. Moran and S. Snir, Efficient Approximation of convex Recolorings. Journal of Computer and System Sciences (JCSS). Volume 73, Issue 7, November 2007, Pages 1078-1089.

  3. S. Moran, S. Snir and K. Sung. Partial Convex Recolorings of Trees and Galled Networks: Tight Upper and Lower bounds. ACM Transactions on Algorithms (TALG).7(4): 42, 2011.

  4. W. Frenkel, Y. Kiat, I. Izhaki and S. Snir. Convex Recoloring as an Evolutionary Marker. Molecular Phylogenetics and Evolution (MPE). 107: 209-220, 2016.

  5. B. Chor, M. R. Fellows, M. A. Ragan, F. A. Rosamond, I. Razgon and S. Snir. “Connected Coloring Completion for General Graphs: Algorithms and Complexity”. COCOON, 2007: 75–85